Regression Analysis
Analyzing probabilities for which there are only two possible outcomes is fairly straightforward. For example, the only two possible outcomes from flipping a coin are either Heads or Tails. Each of these events has an equal 50% probability of occurring.
To analyze more complicated systems having multiple possible outcomes, we need more sophisticated tools. Statisticians use a mathematical tool called regression analysis to make predictions based on past data. Regression analysis reduces a set of data to equations that can be used to accurately describe the data. (The larger the data set, the more accurate the regression and hence, the more accurate the resulting equations). These equations may then be used to forecast future results.
When we plot long-term historical stock market data, we notice a definite pattern:
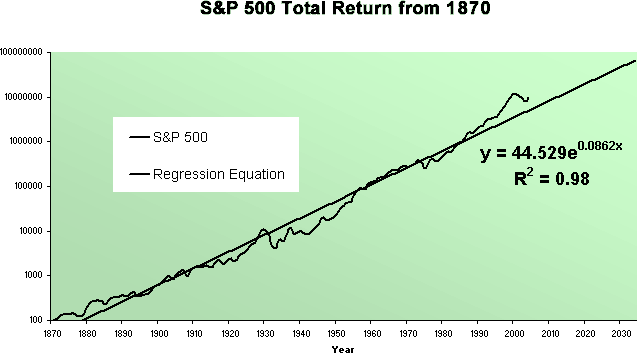
By applying regression analysis to this data set, we discover that we can describe the data set using the following equation:
V(t) = Vo * (1 + long term return)^t +/- Noise
We have already seen that the noise variable is a random term that becomes less significant over time. For long-term investors, we can ignore this term. When we do this, we see that all of our long-term historical stock market data can be approximated by only three variables: an initial value for stocks, a long-term constant return, and time. We have already calculated a long term historical return for stocks at 11% based on Ibbotons' data from 1926 through 2008.
We can now use our formula to do some rough estimates for future levels of the stock market. For example, to estimate where the Dow Jones Industrial Average will be in the year 2033, we can calculate:
DJIA (2038) = DJIA (2008) + (1 + .11) ^ 30
DJIA (2038) = 10,000 + (1+ .11) ^ 30
Solving for DJIA (2033) give us an estimate of 228,000 for the Dow thirty years from now.
Investors control the first variable by making the decision to invest in assets that have historical produced high returns (stocks as opposed to bonds). He controls the second by keeping his portfolio invested through thick and thin for decades.